posted 03-11-2008 03:21 PM            

------------------
Ben

posted 03-11-2008 03:37 PM         

I reviewed the document and didn't see what I was looking for. I will review it again in case I missed it. I suppose I should also clarify a bit.

Specifically, I am looking for any information that states when you report that an examinee demonstrated Significant Responses (SR) to the relevant questions in the test results section, that you also indicate which question or questions they were responding to the most.

I frequently see reports that state an examinee was DI/SR on a multiple issue test and in the same paragraph it indicates that "the question that demonstrated the greatest responses was 'Did you.....'"

posted 03-11-2008 04:28 PM         

You wrote “Specifically, I am looking for any information that states when you report that an examinee demonstrated Significant Responses (SR) to the relevant questions in the test results section, that you also indicate which question or questions they were responding to the most.”

I do not believe you will find a specific answer to your question in a written
‘policy’ form or manual 'that spells it out'. Different examiners are writing their reports in a variety of ways.

As for myself, I “use to” write a line similar to: “Significant Responses were present to a relevant question posed” without identifying the specific relevant question. Then discuss the relevant question being reacted to ‘behind the scenes’ with the therapist/probation. I have changed my report writing style to identify the question\s which showed the ‘Significant Response’ but I also include a paragraph stating I offer ‘No Opinion’ on the remaining relevant questions with an explanation of the reasoning.

Recently I heard Eric Holden speak at a presentation in ref to PCSOT testing. I was rather surprised to hear that he renders a DI / NDI call (as opposed to SR /NSR as recommended in the APA model policy) and identifies the relevant question that the examinee was DI to.

Since I have the presumption Eric is ‘on-top’ of PCSOT- and ‘Best Practices’, I’m beginning to wonder if the APA- PCSOT policy is about to change in the near future and move away from SR/NSR decisions.

If Dan S. is listening in, possibly he could offer another .02 cents.

posted 03-11-2008 05:52 PM         

Done either way, I see potential problems. If no indication is made on the report and another examiner conducts the retest, they are left to make some determination regarding which issue to address, if a specific issue is conducted. Otherwise they are left to conduct the same examination. If an indication is made, there seems to be a tendency for probation officers and therapists to focus too heavily on the one issue, often failing to address the other relevant questions.

cpolys

posted 03-11-2008 07:55 PM            

quote:

---

"The examinee may engage in selective attention which may tune out test questions of a lesser threat."

---

I have a problem with this in particular as is makes little sense to those from whom appropriated the terms. We all learned the term "selective attention" in PSYCH 101. It has to do with two contemporaneous stimuli, only one of which is focused on by the person. In polygraph, we ask the questions 20 to 30 seconds apart (or more). Therefore, no selective attention ca occur.

Scientists told us polygraph can't work because we didn't use correct "controls" in our testing. Our response? Well, they're not controls in the scientific sense..., and they we got laughed at. Some are still laughing.

I'd stick to what we know. We know that the question to which a person reacts the strongest on a multi-issue test isn't necessarily the question to which he's lying. Why? I don't know. We're good at catching liars, but we're poorer when it comes to identifying the lie. To act as if we can do something we can't isn't honest.

I'd simply report which questions had the strongest reactions, and I'd include a standard boiler-plate piece of language that explains what that means and what it doesn't. Just because people want us to sell them a package doesn't mean we should if we have to make things up to satisfy them.

posted 03-12-2008 08:36 AM            

First and foremost the data that Ben had refered to is from the DODPI now DACA, LEPT manual. The manual clearly descibes the scoring for multi-issue testing. The rules state that there is no splitting of calls regarding the outcome of the examination. Most examiners and schools are using and teaching the SR, NSR, and NO decision. No where in the manual does say that one cannot indicate that the most SR was present at a particular question. I also believe that is is safe to call other relevant questions No Opinion is you don't have the necessary scoring criteria to make a call at that particular question.

Can a examinee have SR at one, two, three or four relevant questions? The answer is sure but what is the possibility of that ocurring? This is why it would be best to have or two or three relevant questions in an AFMGQT format. Remember, the DODPI manual states thatyou can have 2,3 or 4 relevant questions.

Those of us who conduct PCSOT exams routinely use an multiple issue testing format. Again we run the risk of the examinee showing more response to one or two questions than all four. We have to stop and think about the theory of psychological set. Where is the examinee going to focus their fears, apprehensions, anxieties, ect? Again this is why I have no problem with reporting to the therapist or PO that the examinee had SR at a particular question. But with that said, I can not state that the other questions showed NSR and clear them of those issues since they tend to be different.

On another note, I believe that Eric has to use NDI, DI and NO becuase of the way the Texas law was written. Keep in mind that the JPCOT rules were written way before the new terms of SR and NSR were coined. Personally, I like the idea of reporting SR, NSR or NO on multiple issue exams. This also includes law enforcement testing. I will still use NDI, DI or NO on a BI-Zone or a two question AFMGQT if both relevant questions address a single issue.

I hope that this helps explains some of the questions that have been raised.

Please keep in mind that I don't have all of the answers, but we have to keep looking at a best practice approach when there are no absolute guidelines established.

Take care

posted 03-12-2008 09:11 AM            

I have long offered my theoretical "Neuro-Lock" test, which combines the DLCT with "Oathing" and "Statement Analysis." This test is based in a more tangible psychophysiological premise---the "lock" being that the examinee reads aloud an oath (no oral cm's), is able to releive innocent emphaticism, is able to compound guilty arousal, is singularly focused on each individual subject via Boca's Region of the brain which enables human's to read and unavoidably focus on the content when it requires reading aloud (the science of neurolinguistics).
Neuro Lock Testing or "oathing" is my combination of what we know--basic polygraph sans pneumos (however they are used for gsr cross-component monitoring)...and what we know of the human brain and how scientists engage examinee's in FMRI labs to "lock" their attentions so that they can review specific brain centers.

This, in my mind , addresses the problem with polygraph (multi-issue).
1. CMs
2. Ping Ponging multi issue phenomena
3. Examinee Insight Seperation
4. psych set challenges with many differing subject targets
5. Examinee focus deficits
6. Examiner voice fluctuations
7. Innocent examinee's being unable to express themselves enough by virtue of a mere "no."
8. Deceptive individuals who need only address a boon of wrongful behavior with ONLY a "no".
9. The nebulous explanations of just what parts of the brain attribute to why polygraph works (the answers to the scientific quandries.)
10. More specificity from oaths than examiner driven questions.Conjunctions allowed.

end of rant....and one more thing....
Where the hell is Spring?

posted 03-12-2008 09:22 AM            

quote:

---

We have to stop and think about the theory of psychological set

---

I agree. The problem is, there is no "theory." In science, a theory is based on a hypothesis (or several hypotheses) or model and evidence that is testable. We have a hypothesis to explain reactions as suggested by Cleve Backster. Let's not forget that the man was a pioneer ahead of his time, but it's crazy to think he, without the requisite training in all the necessary disciplines, could get it all right by himself.

Psych set is a hypothesis that tries to explain why a person reacts to one question more so than others. The problem is that we have evidence to show that doesn't necessarily occur. (Moreover, it's based on fear, something that isn't necessary for polygraph.) In the research on the TES, for example, people lied to one of the CQs yet reacted to the CQ to which they were truthful. Why? I don't know, but it is evidence against psych set - not for it (at least as it's currently defined).

I think it was Dr. Raskin or Kircher who found the same thing with an MGQT study, suggesting that a breakout test on the SR issue was good, but a practice, by itself, that could cause an examiner to make a bad call. Instead, we should do as the DACA manual suggests: Step 1, multi-issue test. If one RQ goes SR, then interview and re-test if no admissions. If NSR, then run original multi-issue, minus the issue broken out for the break out test.

Mark Handler and Ray Nelson wrote a good article in POLYGRAPH back a ways explaining the faults with psych set, and they suggested a better term to help pave the way into greater acceptance in the greater scientific community. Maybe Ray can post it in PDF?

posted 03-12-2008 12:44 PM            

That was a helpful summary.

The tendency to think of someone as "up-on" or "in-the-know" regarding a topic, just because they've been around for a long time, published some important stuff, or wear expensive boots is yet another example of professional imprinting, and should be avoided. This is yet another example of the need for every professional to read both the standards of practice (locally and nationally) and the journal literature. I'm not suggesting anyone is not knowlegeable, just that we all need to read and think for ourselves.

There is still an awful lot that we don't know about PCSOT, and there is a tendency to want to fill in the blanks with something we just made up - just so that we have an answer. Unfortunately, this approach will not impress our adversaries.

Surprisingly little research is occurring regarding PCSOT, and our detractors and oppontents are taking note of that. What you'll see happening, aside from the occassional helpful things like Offe & Offe 2007, is a steady stream of critical and damaging statements in publications from knowledgable and respected persons.

Simple appeals to fear and morality will achieve only temporary victory. Charisma and forceful personalities will not answer the questions of scientists. The long-term solution will be to align our practices with research from risk assessment and risk-management, and not attempt to sway the hearts and minds of scientists and policy makers by making stuff up without proof in the form of sound theory that is cogent with other knowledge, and of course evidence in the form of data.

I would invite anyone to pose an argument about how DI/NSR is more consistent with screening test theory than SR/NSR.

------------------

And now for a thought experiment, and some math.

The LEPET standards, at my last reading, allow for up to five (5) RQs.

We assume that most people are normal in most aspects, because "normal," by definition, is whatever most people are. We then assume they are normal in terms of honesty and integrity, and lifestyle activities. Remember that by "normal" we don't mean a value-based version of normality; we mean "within the normal range," or "within normal limits" when compared to lots of other people from similar socioeconomic, developmental, and cultural backgrounds.

Gaussian theory tells us that 68% of all persons, when evaluating normally distributed data or phenomena, will be within one standard deviation of the population mean, and 95% of all persons will be within 2 standard deviantions. The "normal range" is commonly defined as the wo-standard-deviation range. Therefore 95% of all people are "normal" (i.e., within the normal range, or within normal limits). Only 5% of persons will be considered non-normal, or outside the normal range. This is the basis of the statements of some professionals that delinquency among juveniles is "normal." So 2.5% of persons will be involved in more-than-normal ammoungs of deliquency, and 2.5% of persons can be expected to be involved in a lot less delinquency than those in the normal range.

For some purposes, we use a more conservative normal range of 1 standard deviation, with tells us that 16% of people will be overinvolved in a certain normal activity, and 16% will be underinvolved. We call this a two-tailed experiment, because of the thin tail regions of the dreaded bell curve or normal distribution.

In PCSOT we should be concerned about both tail regions, because that would help us identify persons of low and high risk levels.

In LEPET testing we are really interested in only those persons in one tail region (low risk persons). In a one-tailed experiment, the 84th and 97.5th percentile represent the one standard deviation and two-standard deviation boundaries. What this means is that everyone under the 84th or 97.5th percentile, depending on your tolerance for risk, might not be considered low risk.

So, lets image we are testing police applicants for their history of honesty and integrity: crimes against persons, property crimes, drug use, unlawful sexual activities, and maybe gambling (I don't really know what LEPET targets are - these are what I would, at first thought, imagine as informative for a psychological or risk evaluator)

In mixed-issue screening tests, the RQs are independent. That is, it is conceivable that a person could be deceptive to one or more test questions while being truthful to others. This is conceptual only, and does not imply that mathematical or testing theory can accurate parse both SR and NSR results in a single examination. The statistical principle at work with independent testing targets is called the "multiplication rule." This rule underlies Bayesian theory, and is why paired testing (Marin protocol) is effective. With the multiplication-rule, we estimate the number of anticipated truthful persons, by taking the inverse of the base-rate as the estimated non-deceptive rate, and multiplying that value for each of the investigation targets (RQs). You can see the table below, that when the base-rate is over 15%, for 4 investigation targets, the number of truthful persons falls to 50% or lower. When base-rates are higher, the proportion of truthful persons falls even lower.

It does not surprise me to read at anti-P that some pre-employment screening programs (perhaps those with rigorous standards) have higher rates of failure.

Now factor in what we can estimate about inconclusive rates...

With INC, the statistical priciple at work is not the multiplication-rule, but he "addition-rule" for dependent probability events. Relevant question targets in mixed-issues screening polygraphs are NOT independent regarding INC results. That is because the only unambiguous resolution of a mixed issues exam is when the subject is NSR to all questions. There for any INC response to any target means the test is INC, unless there is something that is SR, in which case all-bets-are-off with everything else that isn't also SR.

With the addition-rule, we add (duh) the estimated INC rate for each distinct investigation target, because any INC result sinks the test.

You can see that INC estimates go up with the number of RQs. These are mathematical realities.

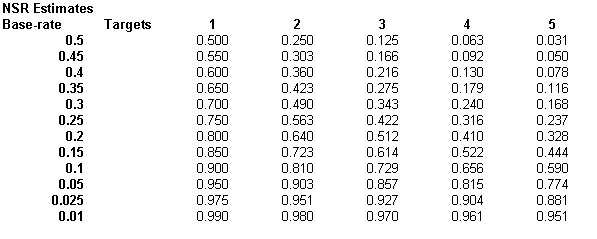
Here is a table of estimates for NSR rates assuming

The solution is not to borrow point or push scores. The solution is to use more advanced statistical procedures which off greater power than the blunt methods we use in present handscoring systems.

Below is a graphic illustrating the results of the OSS training sample, using spot-scoring rules - for which the addition rule plays an important role in the occurrence of INC results. We don't really use spot scoring with ZCT exams, but the data illustrate the point. Using Spot rules, gives 26.7% INC compared with 7.2% INC using two-stage rules.

The point of all this is that we have an obligation to formulate our expections and policies for test performance around an accurate understanding of the mathematical principles that define how and why tests work and what the real limitations are.

r

------------------
"Gentlemen, you can't fight in here. This is the war room."
--(Stanley Kubrick/Peter Sellers - Dr. Strangelove, 1964)